String Angling with Raku
[33] Published 19. September 2019Perl 6 → Raku
This article has been moved from «perl6.eu» and updated to reflect the language rename in 2019.
This is my response to the Perl Weekly Challenge #026.
Challenge #26.1
Let us start programming, and debug later. Or rather, add debug output to help us if it doesn't quite work out:
File: stringcounter-loop
unit sub MAIN (Str $alphabet, Str $string, :$verbose); # [1]
my $count = 0; # [2]
for $alphabet.comb -> $letter # [3]
{
my $current = $string.comb.grep(* eq $letter).elems; # [4]
$count += $current; # [5]
say "$letter: $current "if $verbose; # [6]
}
say $count;
[1] Specify the alphabet, the string and optionally «--verbose».
[2] The total. A variable as I use a loop, and add to it.
[3] Iterate over each letter in the alphabet.
[4] Count the number it occurs in the string. «grep» gives a list of this letter, as many times as it occurs. Adding «.elems» gives the number.
[5] Add the number to the total.
[6] Print the count for each letter, if requested.
Running it:
$ raku stringcounter-loop --verbose chancellor chocolate
c: 2
h: 1
a: 1
n: 0
c: 2
e: 1
l: 1
l: 1
o: 2
r: 0
11
We got 11, and not 8 as expected. The reason is obvious, if we had read the challenge more carefully. The first argument is an alphabet, and alphabets do not have repetitions. (The 3 extra letters come from the duplicate «c» (2) and «l» (1).)
Getting rid of the duplicates in the alphabet does the trick:
File: stringcounter-loop (changes only)
for $alphabet.comb.unique -> $letter
Running it, just to be sure:
$ raku stringcounter-loop chancellor chocolate
8
We can make it considerable shorter if we ditch the debug option:
File: stringcounter-map
unit sub MAIN (Str $alphabet, Str $string);
say $alphabet.comb.unique.map( { $string.comb.grep(* eq $_ ) } ).sum;
I have replaced the «for» loop with a «map», and adding up the numbers from the list by a final «sum».
It is shorter, but definitely harder to understand. It does give the correct answer, but don't take my word for it:
$ raku stringcounter-map chancellor chocolate
8
It is easy to convert it to a one liner (or coerce as it is called in Raku parlance):
File: stringcounter-map-oneliner
say @*ARGS[0].comb.unique.map( { @*ARGS[1].comb.grep(* eq $_ ) } ).sum;
The downside is the missing type checks on the two arguments, and the helpful names they had.
«Keep it simple»
You may have noticed that I have ignored the last lines of the the challenge: «To keep it simple, only A-Z,a-z characters are acceptable. Also make the comparison case sensitive».The last one is ok, but the first one is trickier. It is presented «to keep it simple», but adding a check for it in my program will only add complexity. Code complexity.
Well. I'll just add the check with the help of a custom type:
File: stringcounter-subset
subset AtoZ of Str where /^ <[A .. Z a .. z]>+ $/; # [1]
unit sub MAIN (AtoZ $alphabet, AtoZ $string);
say $alphabet.comb.unique.map( { $string.comb.grep(* eq $_ ) } ).sum;
[1] One or more characters (specified with «+») in the range «A..Z a..z», and it must match the entire string (the «^» and «$» anchors).
It is possible to write it much clearer, using Sets.
A Very Short Set Introduction
A «Set» (which you probably learned about in mathematical class at school) is a simplified version of a Raku hash. The keys are all there is to it; either an element is in the «Set» or it isn't. Adding an element addional times makes no difference.A «Bag» is a variant of «Set», with an integer as the value. This integer is the weight, or counter. Adding a value additional times increases the weight.
File: stringcounter
subset AtoZ of Str where /^ <[A .. Z a .. z]>+ $/;
unit sub MAIN (AtoZ $alphabet, AtoZ $string);
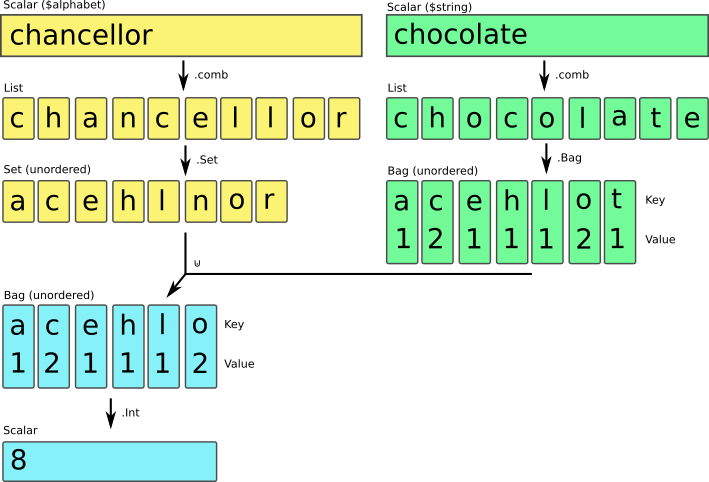
say ($alphabet.comb.Set ⊍ $string.comb.Bag).Int;
# #1 #3 #2 #4
[1] We turn the alphabet string (or rather, the individual characters) into a «Set». This gets rid of duplicates.
[2] We turn the string (again as individual characters) into a «Bag». Duplicates are kept in the values.
[3] The «Baggy multiplication
operator» ⊍ multiplies the weights of the left hand side with the
right hand side, acting as a filter to only let through values on both sides
(characters in the alphabet and the string). The left hand value
isn't a «Bag», but the operator coerces it to one automatically.
[4] Reduce the «Bag» to an Int. This gives us the sum of all the weights, which is exactly what we are looking for.
See docs.raku.org/language/setbagmix for more information about Set, Bag (and some other types).
See docs.raku.org/language/operators#infix_(.),_infix_⊍ for more information about the «Baggy multiplication operator».
An illustration may make it clearer:
Challenge #26.2
Create a script that prints mean angles of the given list of angles in degrees. Please read wiki page that explains the formula in details with an example.
The wikipedia article presents two formulas, and I chose this one:

Let us start programming:
File: mean-angles
unit sub MAIN (*@angles); # [1]
my \n = @angles.elems; # [2]
my @rad = @angles.map({$_ * pi / 180 }); # [3]
my \s = @rad.map(*.sin).sum / n; # [4]
my \c = @rad.map(*.cos).sum / n; # [5]
my $mean = atan2( s / c ) * 180 / pi; # [6]
if c < 0 { $mean += 180; } # [7]
elsif s < 0 { $mean += 360; } # [7]
say "mean: $mean"; # [8]
[1] The program takes a list of angles as argument, so we use a slurpy argument to get them in an array.
[2] The number of arguments (and angles). Note the sigil-less variable name.
[3] The angles are specified in degrees, but we need them in radians as that is used by the «sin» and «cos» commands. Using «map» saves us a «for» loop. Note that «pi» is built-in.
[4] This follows from the formula, the sum of the sine value of all the angles, divided by the number of angles.
[5] The same for the cosine part.
[6] And finally, the mean. The last part transforms the angle back to degrees.
[7] This correction of the angle is presented in the «Example» section of the wikipedia article.
[8] And finally, we print the mean angle.
We can get rid of the curlies inside the «map» if we use a whatever star, like this:
my @rad = @angles.map(* * pi / 180);
It is shorter, but not nesessarily easier to understand.
Running it, with the sample angles from the wikipedia article:
$ raku mean-angles 10 20 30
mean: 19.999999999999996
$ raku mean-angles 355 5 15
mean: 4.9999999999999964
Note the rounding error. The result should have been «20» and «5». The problem is the floating point type «Num» used for the computations. Using the powerful «FatRat» type (which supports an almost limitless number of digits) instead doesn't help, as «sin» gives a «Num» and by then the damage has been done.
The solution is to reimplement «sin», «cos», «atan2» and the rest of them to use «FatRat», or rather write a module which gives «FatRat» versions of them. That is not something I'd do voluntarily, so that's it for now.