DIY Cryptography with Perl 6
Part 1: Base 36
[8.1] Published 21. April 2019Perl 6 → Raku
This article has been moved from «perl6.eu» and updated to reflect the language rename in 2019.
See also: The Introduction.
At the end of the Raku from Zero to 35 article I introduced an alphabet consisting of 42 letters, and showed code to convert from base 10 to base 42 and vice versa. That got me thinking about using it to encrypt texts.
We can use Base 36, which uses 0..9 and A..Z as digits (or "digits"), to convert a simple text with the built in «parse-base» like this (in REPL):
$ raku
> say "ARNE".parse-base(36); # -> 502394
> say "Arne".parse-base(36); # -> 502394
Note that parse-base considers lower-
and uppercase letters equal.
The other direction (also in REPL):
> say 502394.base(36); # -> ARNE
The Value of the Base
You can skip this section if you do not want to know how positional number systems work, or if you already know.
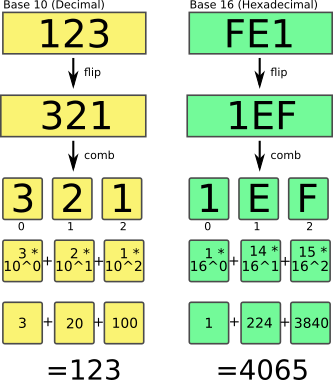
Now do the same for for the base 16 (hexadecimal) example. The digits «A» to «F» come after 0-9, and have the decimal values 10 to 15. You can check the result like this:
> say "FE1".parse-base(16); # -> 4065
Base 40, Custom Made
So far so good, but we need some punctuation characters to make it possible to encode anything other than a single word. I did just that in the base 42 example (in the Raku from Zero to 35 article), but the additional letters «Æ», «Ø», «Å», «Ä», «Ö» and «ß» are no good in this context. The encode and decode functions from that article is used here with minor changes. See that article for an explanation of the code.
I have chosen a bare minimum of punctuation characters; « » (a single space), «.» (a period), «?» (a question mark) and «!» (an exclamation mark), making it a total of 40 characters:
File: encode40
constant @base40 := (0 .. 9, "A" .. "Z", " ", ".", "?", "!").flat;
subset Alphabet of Str where { /^@base40+$/ };
my %values = @base40.map( { $_ => $++ } );
sub MAIN (Alphabet $base40string)
{
say $base40string.flip.comb.map( {%values{$_} * 40 ** $++ } ).sum;
}
Running it:
$ raku encode40 "ARNE SOMMER"
112088664946083787
Note that I used the expression «encode», and not «encrypt», as I use a one to one mapping between a character and a value. I'll explain why that is problematic in the next section.
Then the other direction, as encoding without also offering decoding wouldn't make much sense:
File: decode40
constant @base40 := (0 .. 9, "A" .. "Z", " ", ".", "?", "!").flat;
say @base40[10];
sub MAIN (Int $number is copy, :$debug = False)
{
my @result;
while $number
{
@result.push($number % 40); # The remainder
$number = $number div 40; # Integer division
}
say @result.reverse if $debug;
say @base40[@result.reverse].join;
}
Running it:
$ raku decode40 112088664946083787
ARNE SOMMER
Cryptography vs Encoding
It is easy to break the encryption, especially if it has been used to send a long message - or if it has been used to send several short messages.The main problem is that it isn't actually encryption at all, but merely encoding. A single letter gets the same encoding all the time. That is a problem because an attacker can use Letter Frequency Analysis to guess the mapping. And the mapping in this case is in alphabetical order, making it even easier.
The trick of displaying the encoded message as a number, and not a sequence of integers
isn't very original - and is easy to guess. You can see the actual values used, after
removing the integer wrapping (applied by base 40) if you want to, with the
--debug flag:
$ raku decode40 --debug 112088664946083787
(10 27 23 14 36 28 24 22 22 14 27)
ARNE SOMMER
The encoding algorithm doesn't add message authentication, so if somebody managed to intercept the message and change it before sending it on, the recipient wouldn't know that it had been tampered with.
Changing the value can mess up the entire message, but not always:
$ raku decode40 --debug 112088664946083782
(10 27 23 14 36 28 24 22 22 14 22)
ARNE SOMMEM
$ raku decode40 --debug 11208866494608378
(1 2 30 13 19 26 34 18 10 9 18)
12UDJQYIA9I
In the first one I changed the last digit (from 7 to 2), and in the second one I removed the last digit.
Making a decoder when you have the numbers is quite easy:
$ raku
> constant @base40 := (0 .. 9, "A" .. "Z", " ", ".", "?", "!").flat;
> say @base40[<10 27 23 14 36 28 24 22 22 14 27>].join
ARNE SOMMER
Using a one to one mapping to encode a message is almost as bad as sending the message as plain text. The downside is that the recipient and receiver may think that the communication is secure, and it isn't. The upside is that somebody that just happens to see the message in transit cannot accidentally learn something, as it takes an active action (decode it) to get the message.
Part 2: Base 400
See the next part; Part 2: Base 400.